Tensorflow guida italiano intende essere una guida in italiano per muovere i primi passi con Tensorflow, una libreria per il Machine Learning e il Deep Learning giunta alla versione di Tensorflow 2.0.
In Tensorflow 2: how to start? abbiamo seguito un esempio semplice, riproducendo una rete neurale artificiale per la conversione delle temperature.
Puoi trovare questo Tensorflow Tutorial in italiano qui.
Udacity ha invece sviluppato un corso tensorflow gratuito che puoi trovare qui.
Ok dovrebbe bastare.
Bentornato!
Possiamo finalmente iniziare a macinare informazioni utili, dopo aver accuratamente studiato un’introduzione SEO-friendly ricca di keywords per i crawler di Google, i bot usati nell’indicizzazione delle pagine web (Qui una spiegazione dettagliata).
Caro il mio marinaio, è giunto il momento di salpare alla volta di tensori, reti neurali, grafi e operazioni di derivazione.
Questa è la Tensorflow Guida in Italiano. Iniziamo!
Tensorflow Guida Italiano
First thing first: where can I code?
Tensorflow è piattaforma Open Source per Python, che consente lo sviluppo di sistemi di machine learning. Esiste anche una versione Web, chiamata Tensorflow.js, che per il momento non consideriamo.
Per iniziare a muovere i primi passi con Tensorflow hai bisogno di un ambiente Python configurato: in alternativa puoi avviare un documento Google Colab Online, che contiene tutto il necessario per programmare fin da subito.
In tal caso, ho realizzato per te questa breve guida che ti insegna a prendere dimestichezza con i Jupyter Notebook di Google Colab.
Prima cosa da fare: importare la versione più recente di Tensorflow.
Il 27 Marzo 2020 è stato compiuto lo switching della default version della libreria, passata dalla 1.x alla 2.x, rendendo superfluo andare a specificare quale versione importare.
Ci basta quindi scrivere:
# import Tensorflow import tensorflow as tf # for numerical computation and plotting import numpy as np from matplotlib import pyplot as plt
Ora, devi sapere una cosa.
Tensorflow è una parola composta da Tensor e flow
La prima indica un tensore, vale a dire una struttura dati generale definita da un singolo spazio vettoriale, di cui vettori, matrici, funzioni lineari ed endomorfismi costituiscono casi particolari.
La seconda indica il flusso che viene seguito per il calcolo di operazione complesse.
Tensorflow si configura quindi come un framework per la definizione e il calcolo di operazioni che coinvolgono tensori, rappresentazioni generiche di vettori e matrici a dimensioni maggiori.
Internamente, Tensorflow rappresenta i tensor come array n-dimensionali di datatypes base (int, string, etc..)
Esistono alcuni tensori particolari, tra cui:
tf.Variable(
initial_value=None, trainable=None, validate_shape=True, caching_device=None,
name=None, variable_def=None, dtype=None, import_scope=None, constraint=None,
synchronization=tf.VariableSynchronization.AUTO,
aggregation=tf.compat.v1.VariableAggregation.NONE, shape=None
)
tf.constant(
value, dtype=None, shape=None, name='Const'
)A eccezione del tf.Variable, i tensori sono immutabili.
Shape and Rank
Devi sapere che ogni elemento in un tensor condivide poi il data type, che è sempre noto, con quello degli altri elementi.
La shape di un tensor (vale a dire il numero di dimensioni e la lunghezza di ogni dimensione) può invece essere anche parzialmente nota.
Questo perché la maggior parte delle operazioni produce tensori di dimensioni completamente note (full-known) se quelle degli input sono altrettanto conosciute. In altri casi è possibile determinare la shape finale solo al termine dell’esecuzione dei grafi.
Un grafo è la rappresentazione, per mezzo di nodi, di operazioni eseguite sui tensori.
Il rank di un tensor è invece il numero di dimensioni (n-dimenions), e può essere considerato l’ordine di grandezza del tensore.
Per maggiori info, la documentazione è ricca di spunti.
Facciamo comunque qualche esempio:
# create 1-d Tensors from vectors and lists
sports = tf.constant(["Tennis", "Basketball"], tf.string)
numbers = tf.constant([3.141592, 1.414213, 2.71821], tf.float64)
print("`sports` is a {}-d Tensor with shape: {}".format(tf.rank(sports).numpy(), tf.shape(sports)))
print("`numbers` is a {}-d Tensor with shape: {}".format(tf.rank(numbers).numpy(), tf.shape(numbers)))
# Output:
#`sports` is a 1-d Tensor with shape: [2]
#`numbers` is a 1-d Tensor with shape: [3]Perfetto.
Abbiamo preso dimestichezza con gli elementi base, i tensori, ora è arrivato il momento di passare all rappresentazione di tensor dalle dimensioni maggiori.
In applicazioni reali, come vedremo, avremo bisogno anche di 4-d Tensor, con i quali rappresentare ad esempio immagini in task di image preprocessing e computer vision.
Consideriamo dunque un tensor pronto a gestire 10 immagini quadrate a colori di 256px nello spazio RGB: 10 x 256*256*3.
'''Define a 4-d Tensor.''' # Use tf.zeros to initialize a 4-d Tensor of zeros with size 10 x 256 x 256 x 3. # You can think of this as 10 images where each image is RGB 256 x 256. # Creates a tensor with all elements set to zero. images = tf.constant(tf.zeros((10,256,256,3), tf.int32, "The name of the operation")) assert isinstance(images, tf.Tensor), "matrix must be a tf Tensor object" assert tf.rank(images).numpy() == 4, "matrix must be of rank 4" assert tf.shape(images).numpy().tolist() == [10, 256, 256, 3], "matrix is incorrect shape"
Computations | Tensorflow Guida Italiano alle operazioni
Per comprendere il flow dei dati e delle operazioni in Tensorflow, possiamo servirci dei grafi, rappresentazioni convenienti di computazioni.
Un grafo, o graph, e sarà quindi costituito da tensori, che gestiranno i dati, e dalle operazioni compiuti su di essi.
Vediamo una semplice operazione di somma: due tensori costanti e una sommatoria.
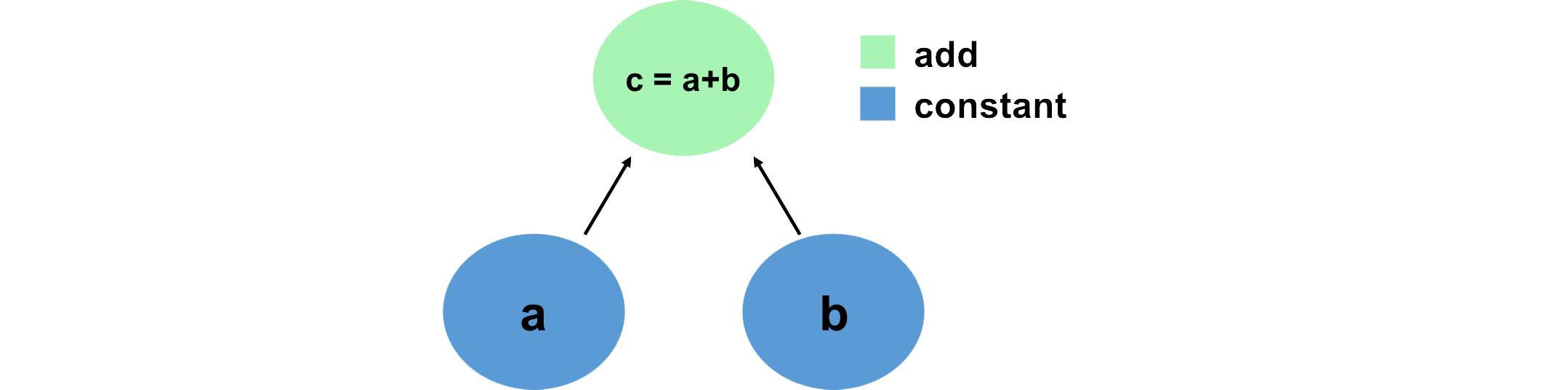
# Create the nodes in the graph, and initialize values a = tf.constant(15) b = tf.constant(61) # Add them! c1 = tf.add(a,b) c2 = a + b # TensorFlow overrides the "+" operation so that it is able to act on Tensors print(c1) print(c2) # Output: # tf.Tensor(76, shape=(), dtype=int32) # tf.Tensor(76, shape=(), dtype=int32)
Ora consideriamo un esempio più complesso:
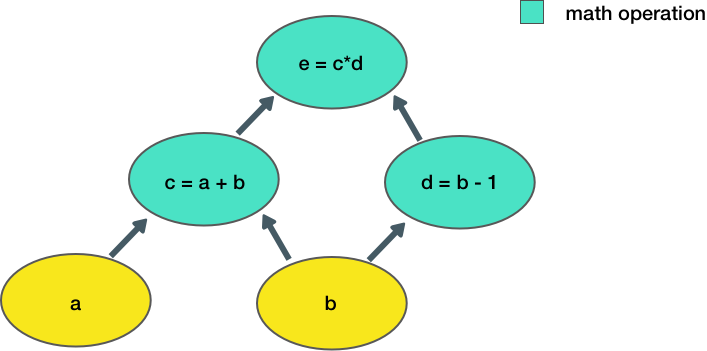
Andiamo ora a costruire una funzione che riproduca le operazioni rappresentate nel grafo:
'''Defining Tensor computations'''' # Construct a simple computation function def func(a,b): c = tf.add(a,b) d = tf.subtract(b,1) e = tf.multiply(c,d) return e
Quindi calcoliamo il risultato:
# Consider example values for a,b a, b = 1.5, 2.5 # Execute the computation e_out = func(a,b) print(e_out) # Output: # tf.Tensor(6.0, shape=(), dtype=float32)
L’ouput è un semplice scalare, privo di dimensoni.
Tensorflow Guida Italiano alle Neural Network
Ovviamente, possiamo andare definire delle reti neurali artificiali ed eseguire operazioni complesse grazie a loro.
Devi sapere che Tensorflow usa una high-level API chiamata Keras, di cui abbiamo parlato in passato, che fornisce una potente e intuitiva interfaccia per creare e allenare reti neurali profonde, o Deep Neural Network
Nella nostra splendida introduzione al machine learning, che ti consiglio caldamente di leggere, così come in quella sulle reti neurali artificiali, che trovi invece qui, abbiamo descritto il perceptron.
Per semplicità, lo rappresenteremo graficamente come segue:
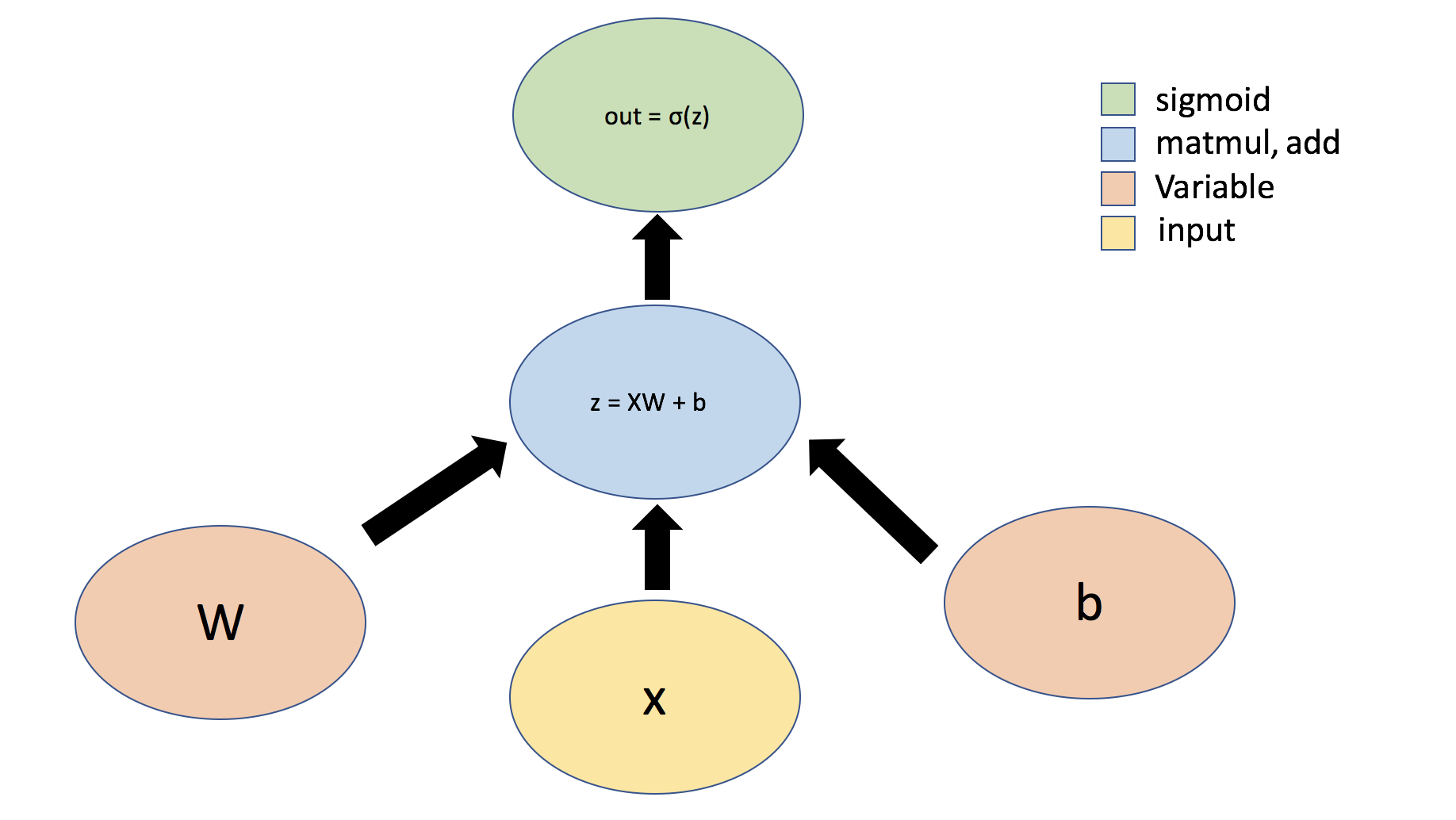
I tensor possono essere organizzati in Layer.
Secondo la documentazione ufficiale, un layery (a livello di tensorflow) è un classe che implementa operazioni comuni per le reti neurali quali convoluzione, gestione dei weight, dei loss e degli aggiornmenti generici.
Usiamo la struttura sottostante per definire un Layer e implementare il perceptron:
### Defining a network Layer ###
# n_output_nodes: number of output nodes
# input_shape: shape of the input
# x: input to the layer
class OurDenseLayer(tf.keras.layers.Layer):
def __init__(self, n_output_nodes):
super(OurDenseLayer, self).__init__()
self.n_output_nodes = n_output_nodes
def build(self, input_shape):
d = int(input_shape[-1])
# Define and initialize parameters: a weight matrix W and bias b
# Note that parameter initialization is random!
self.W = self.add_weight("weight", shape=[d, self.n_output_nodes]) # note the dimensionality
self.b = self.add_weight("bias", shape=[1, self.n_output_nodes]) # note the dimensionality
def call(self, x):
'''TODO: define the operation for z (hint: use tf.matmul)'''
z = tf.matmul(x,self.W) + self.b
'''TODO: define the operation for out (hint: use tf.sigmoid)'''
y = tf.sigmoid(z)
return y
# Since layer parameters are initialized randomly, we will set a random seed for reproducibility
tf.random.set_seed(1)
layer = OurDenseLayer(3)
layer.build((1,2))
x_input = tf.constant([[1,2.]], shape=(1,2))
y = layer.call(x_input)
# test the output!
print(y.numpy())
mdl.lab1.test_custom_dense_layer_output(y)
# Output:
# [[0.26978594 0.45750412 0.66536945]]
# [PASS] test_custom_dense_layer_output
# TruePer convenienza, Tensorflow ha definito una serie di Layer comuni risparmiandocene in questo modo la codifica da zero.
Un esempio è il Dense Layer. (doc)
Per organizzare più layer, possiamo impiegare un modello di Keras chiamato Sequential (doc). Con questa API possiamo facilmente impilare più livelli e definire la nostra neural network.
''' Defining a neural network using the Sequential API ''' # Import relevant packages from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense # Define the number of outputs n_output_nodes = 3 # First define the model model = Sequential() '''Define a dense (fully connected) layer to compute z''' # Remember: dense layers are defined by the parameters W and b! # You can read more about the initialization of W and b in the TF documentation :) # https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dense?version=stable dense_layer = Dense(n_output_nodes) # Add the dense layer to the model model.add(dense_layer)
Ora possiamo testare la nostra rete usando un piccolo input:
# Test model with example input x_input = tf.constant([[1,2.]], shape=(1,2)) '''feed input into the model and predict the output!''' model_output = model.predict(x_input) print(model_output) # Output: # [[ 0.24415088 0.6485772 -1.9461871 ]]
In generale, useremo la Layer class per definire blocchi computazionali interni e la Model class per definre il modello esterno: l’oggetto da allenare.
In una variazione della ResNet, di cui abbiamo parlato qui, la ResNet50 ci sono diverse sottoclassi di modelli ResNet e una solo Model Class finale, quella che chiamiamo rete o modello.
Guida Tensorflow Italiano alle Subclass: ecco le sottoclassi
Per rendere la nostra Tensorflow Guida Italiano, degna di nota non possiamo non parlare delle sottoclassi.
Usando le sottoclassi possiamo creare diverse classi per il nostro modello, e poi definire il forwardpass attraverso la rete con la funzione call.
Le sottoclassi ci permettono di definire custom layer, custom training loops, custom activation function e custom model.
Ora ricreiamo la rete neurale precedente sostituendo le sottoclassi al Sequential Model
''' Defining a model using subclassing '''
from tensorflow.keras import Model
from tensorflow.keras.layers import Dense
class SubclassModel(tf.keras.Model):
# In __init__, we define the Model's layers
def __init__(self, n_output_nodes):
super(SubclassModel, self).__init__()
'''TODO: Our model consists of a single Dense layer. Define this layer.'''
self.dense_layer = Dense(n_output_nodes)
# In the call function, we define the Model's forward pass.
def call(self, inputs):
return self.dense_layer(inputs)
Ora testiamolo!
n_output_nodes = 3 model = SubclassModel(n_output_nodes) x_input = tf.constant([[1,2.]], shape=(1,2)) print(model.call(x_input)) # Output: # Tf.Tensor([[ 0.62118787 -0.08692831 1.6387595 ]], shape=(1, 3), dtype=float32)
Le sottoclassi estendono le nostra capacità garantendoci una flessibilità pressoché infinita.
In questo potremmo ad esempio condizionare il ritorno della funzione call, modificando il comportamento della rete durante il training e l’inferenza.
Ad esempio, supponiamo di voler ritornare l’input senza alcuna perturbazione in alcune circostanze. Definiamo un argomento booleano nella funzione call che controlli questo comportamento:
''' Defining a model using subclassing and specifying custom behavior '''
from tensorflow.keras import Model
from tensorflow.keras.layers import Dense
class IdentityModel(tf.keras.Model):
# As before, in __init__ we define the Model's layers
# Since our desired behavior involves the forward pass, this part is unchanged
def __init__(self, n_output_nodes):
super(IdentityModel, self).__init__()
self.dense_layer = tf.keras.layers.Dense(n_output_nodes, activation='sigmoid')
'''TODO: Implement the behavior where the network outputs the input, unchanged,
under control of the isidentity argument.'''
def call(self, inputs, isidentity=False):
x = self.dense_layer(inputs)
'''TODO: Implement identity behavior'''
return inputs if isidentity else x
Quindi eseguiamo il codice e gustiamoci il risultato:
n_output_nodes = 3
model = IdentityModel(n_output_nodes)
x_input = tf.constant([[1,2.]], shape=(1,2))
'''TODO: pass the input into the model and call with and without the input identity option.'''
out_activate = model.call(x_input)
out_identity = model.call(x_input,isidentity=True)
print("Network output with activation: {}; network identity output: {}".format(out_activate.numpy(), out_identity.numpy()))
# Output:
# Network output with activation: [[0.11969814 0.43011418 0.3474862 ]]; network identity output: [[1. 2.]]
Ora che sappiamo come definire nuovi Layer e costruire neural network in Tensorflow usando sia la Sequential API che la Subclass API è arrivato il momento d’implementare l’algoritmo di backpropagtion.
Guida Tensorflow per l’Automatic Differentiation
Un concetto chiave nel processo di training di una neural network, è quello di calcolo dell’errore compiuto nella previsione, e della sua retropropagazione ai layer precedenti.
Devi sapere che questi sono concetti fondamentali.
Sono veloce perché ne abbiamo ampiamente parlato nel post dedicato alla teoria delle reti neurali artificiali, che trovi qui.
Per il momento sappi che a livello matematico, l’allenamento di una rete neurale richiede che vengano eseguite operazioni computazionali, più o meno complesse, come il calcolo differenziale di una funzione.
La differenziazione automatica ci viene in aiuto.
Per Automatic Differentiation intendiamo allora un insieme di tecniche per calcolare la derivata di una funzione attraverso la Regola della Catena(chain rule).
Per mezzo di operazioni elementari (addizione, sottrazione etc…) e funzioni basilari (exp, log, etc…), consente di determinare una qualsiasi derivata, in modo preciso ed efficiente.
Questo insieme di tecniche è alla base dell’algoritmo di backpropagation.
Tensorflow Gradient Tape
Per ottimizzare la ricerca del minimo globale (global optima) della funzione di costo (objective function) esistono diversi algoritmi di ottimizzazione (trattai qui), di cui la discesa del gradiente (gradient descent) ne è il più comune. (come abbiamo visto qui).
Per il calcolo del gradiente in Tensorflow, abbiamo bisogno di un record delle operazioni compiute: tf.GradientTape (doc) corre in soccorso.
Quando il flusso è compiuto in avanti, espressione italiana aberrante per indicare il forward-pass o feed-forward system, tutte le operazioni sono ricordate su un tape.
Poi, il gradiente è calcolato svolgendo all’indietro il tape delle operazioni.
Ogni singolo tf.GradientTape può quindi calcolare un solo gradiente, in alternativa possiamo creare un persistent gradient tape e calcolare più gradienti.
Definiamo una semplice funzione quadratica e calcoliamone il gradiente (la derivata):
''' Gradient computation with GradientTape ''' # y = x^2 # Example: x = 3.0 x = tf.Variable(3.0) # Initiate the gradient tape with tf.GradientTape() as tape: # Define the function y = x * x # Access the gradient -- derivative of y with respect to x dy_dx = tape.gradient(y, x) assert dy_dx.numpy() == 6.0
Nel prossimo blocco di codice useremo lo SGD (qui la spiegazione) per calcolare il minimo della objective function:
[latexpage]
$$ L=(x-x_f)^2 $$
xf è la variabile per il valore che vogliamo ottimizzare; L rappresenta la nostra funzione costo che intendiamo minimizzare.
Calcoliamo il risultato usandoGradientTape, benché sia possibile in questo caso risolverlo analiticamente, per preparare la strada a lavori futuri.
''' Function minimization with automatic differentiation and SGD '''
# Initialize a random value for our initial x
x = tf.Variable([tf.random.normal([1])])
print("Initializing x={}".format(x.numpy()))
learning_rate = 1e-2 # learning rate for SGD
history = []
epochs = 300
# Define the target value
x_f = 4
# We will run SGD for a number of iterations. At each iteration, we compute the loss,
# compute the derivative of the loss with respect to x, and perform the SGD update.
for i in range(epochs):
with tf.GradientTape() as tape:
'''TODO: define the loss as described above'''
loss = (x - x_f)*(x - x_f)
# loss minimization using gradient tape
grad = tape.gradient(loss, x) # compute the derivative of the loss with respect to x
new_x = x - learning_rate*grad # sgd update
x.assign(new_x) # update the value of x
history.append(x.numpy()[0])
# Plot the evolution of x as we optimize towards x_f!
plt.plot(history)
plt.plot([0, epochs],[x,x_f])
plt.legend(('Predicted', 'True'))
plt.xlabel('Iteration')
plt.ylabel('x value')
# Output:
# Initializing x=[[-0.92759573]]
# Text(0, 0.5, 'x value')
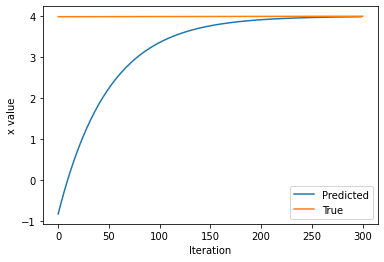
Per sfruttare appieno le potenzialità dell’algoritmo di retropropagazione dell’errore, tracciamo i flussi in avanti (forward pass) sul tape, usiamo l’informazione per determinare il gradiente e infine questi gradienti per l’ottimizzazione attraverso il SGD.
Primi passi con tensorflow: il tuo primo progetto
Ora puoi finalmente cimentarti in qualcosa di concreto.
In questa Guida Tensorflow hai visto gli elementi fondamentali di questo framework.
Seguimi allora in quello che sarà il tuo primo progetto!
Andremo a realizzare una piccola rete neurale, e poi una più complessa rete neurale convoluzionale, per classificare alcune immagini.
TensorFlow MNIST Tutorial con CNN, la guida in italiano step by step per creare una CNN!
Tensorflow Guida: domande frequenti sui primi passi!
Ho pensato di raccogliere per te alcune domande e relative risposte sull’argomento: penso le troverai utili!
Per il momento è tutto!
Per aspera, ad astra.
Un caldo abbraccio, Andrea.




