Il Markov Decision Process (MDP) o processo decisionale di Markov è un modello di gestione dello stato di transizione di un agente in un ambiente dinamico e casuale, dunque non deterministico.
Fornisce un modello matematico per modellare un processo decisionale in quelle situazioni in cui il risultato è parzialmente casuale (random), e in parte sotto controllo di un decisore (decision maker).
Una definizione molto comoda per compiacere il nostro interlocutore, ma poco utile per comprendere a fondo il significato di questo concetto.
Dobbiamo scendere più a fondo.
I mariani hanno ricevuto ordini.
Cambusa riempita e vele spiegate: siamo pronti per questo nuovo viaggio!
Scopriamo insieme in cosa consiste il Markov Decision Process, e sopratutto perché sia importante.
Markov Decision Process
Per capire a fondo cosa sia un processo decisionale di markov dobbiamo fare chiarezza su almeno due conceti:
- La catena di Markov, o Markov chain
- La proprietà di Markov o Markov property
Iniziamo dal primo.
Markov Chain
Nei primi anni del secolo scorso, il matematico russo Andrej Markov studiò i processi stocastici, che involvono un elemento di casualità, senza memoria, chiamati catene di Markov o Markov Chains.
Un tale processo ha un numero fisso di stati, ed evolve in modo casuale da uno stato all’altro, a ogni step.
La probabilità che l’evoluzione avvenga dallo stato s a quello s’ è fissa e dipende unicamente dalla coppia (s, s’) e non dagli stati passati, ergo per cui definiamo il sistema come privo di memoria.
Privo di memoria?
No, non ha bevuto la sera prima e dimenticato la festa in spiaggia tornando a casa con un male alla testa da Guiness World Record.
Possiamo però fare chiarezza sull’argomento.
Markov Property
Tecnicamente, l’indipendenza dagli stati passati in un processo stocastico è definita in Teoria della Probabilità come Markov property, trovi un approfondimento qui.
La Markov Property è il discriminante per distinguere i Markov Process.
Diciamo infatti che un processo stocastico si definisce Markov Process se e solo se risulti caratterizzato dalla Markov Property, e quindi se la distribuzione di probabilità condizionata dei futuri stati del processo (condizionata su entrambi gli insiemi di stati futuri e passati) dipende unicamente dallo stato presente e non dalla sequenza di eventi precedenti.
Devi sapere anche un’altra cosa fondamentale.
Da un punto di vista matematico, un processo stocastico altro non è che una famiglia di variabili casuali (i.e. Il cui valore dipende da un fenomeno aleatorio, cioè casuale) indicizzate da un parametro temporale.
Distinguiamo allora un processo stocastico tempo-discreto (o tempo-continuo) a seconda che lo spazio della variabile tempo sia discreto (o continuo).
Ora hai tutti gli strumenti per capire cosa sia davvero una Markov chain: un processo stocastico tempo-discreto (i.e. Discreto nel tempo) che soddisfa la Markov property.
Le Markov chains sono utilizzate in molte aree, tra cui termodinamica, chimica, statistica e altre.
Vediamo ora cosa sia un Markov decision process.
Markov Decision Processes
Fu Richard Bellman a descrivere per la prima volta i Markov Decision Processes in una celebre pubblicazione degli anni ’50.
I Markov Decision Processes sono allora un’estensione delle Markov Chains, con due aggiunte:
- Azioni, actions (i.e. Permettono una scelta)
- Ricompense, rewards (i.e. Motivano l’agente)
Quando esiste una sola azione per ogni step, e tutte le ricompense sono uguali, il processo decisionale di Markov (Markov decision process) si riduce a una catena di Markov (Markov chain).
Osserviamo allora un esempio di Markov decision process.
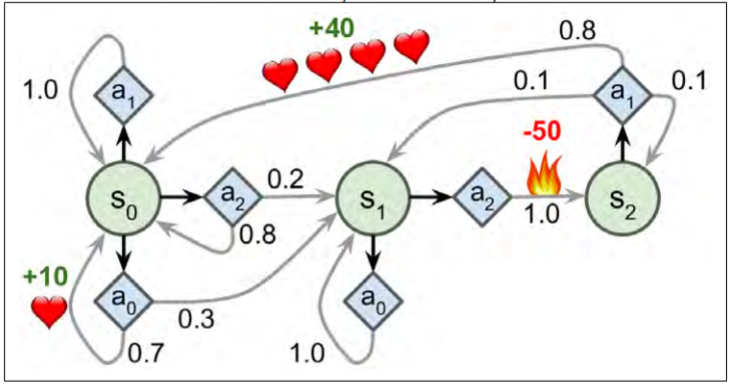
Il MDP in figura ha 3 stati e al massimo 3 azioni per ogni step.
Iniziando allo stato s0 l’agente può scegliere una delle 3 azioni a0,a1,a2.
Se scegliesse l’azione a1 rimarrebbe nello stato s0 con certezza (probabilità 1.0) senza ottenere alcuna ricompensa.
Se scegliesse l’azione a0, avrebbe il 70% di probabilità di guadagnare una ricompensa di 10 punti e rimanere nello stato s0. In questo caso l’agente potrebbe optare per la medesima scelta ottenendo quante più ricompense possibili, benché a un certo punto raggiungerà lo stato s1.
Nello stato s1 le azioni sono 2: a0 e a2.
L’agente può ora scegliere di stare ripetutamente nello stato optando per l’azione a0. L’azione a2 permetterebbe invece all’agente di raggiungere lo stato s2 seppur con una ricompensa negativa di 50 punti.
Dallo stato s2 la sola azione concessa è l’a0 che riporterebbe l’agente allo stato iniziale con una ricompensa di 40 punti.
Bellman individuò un modo per stimare un parametro, l’optimal state value di qualunque stato s, espresso come V*(s) inteso come somma di tutte le future ricompense scontate (i.e. Con applicato il discount rate, spiegato in questo post) che l’agente può potenzialmente ricevere in media dopo aver raggiunto lo stato s, assumendo che agisca in modo ottimale.
Bellman dimostrò che quando l’agente agisce in modo ottimale, la Bellman Optimality Equation può essere applicata.
Si tratta di un’equazione ricorsiva che, assumendo che l’agente agisca in modo ottimale, permette il calcolo dell’optimal state value, dello stato corrente come la somma delle ricompense che potrebbe ottenere in media optando per l’azione ottimale e la stima dell’optimal state value di tutti i possibili stati a cui l’azione designata porterebbe.
Questa equazione conduce a un algoritmo in grado di stimare precisamente l’optimal state value di ogni possibile stato: inizializzando ogni parametro a zero, e aggiornandoli iterativamente usando il Value Iteration Algorithm.
Il punto di forza di questo metodo è la garanzia che i valori stimati convergano all’optimal state values di ogni stato, costituendo dunque la policy ottimale.
Per il momento è tutto.
Per aspera, ad astra.
Un caldo abbraccio, Andrea.




