Ridge Regression, chiamato anche Tikhonov regularization, è una versione regolarizzata della Regressione Lineare (linear regression): aggiungendo un termine di regolarizzazione (regularization term), comunemente denominato alpha, alla cost function, l’algoritmo di apprendimento viene forzato a tenere i weight quanto più bassi possibili.
Abbiamo iniziato in quinta, ma per un motivo chiaro: avendo fornito una definizione come introduzione ti sarà facile ripassare quando un giorno tornerai su questo post unicamente per lei.

Ora però ci prendiamo un po’ di tempo per allinearci e procedere a comprendere davvero cosa sia la Ridge Regression.
Ridge Regression: why?
Il miglior modo per comprendere la Ridge Regression è capire perché esista.
Quando ci allontaniamo dalle sfide di Kaggle per addentrarci in quella giungla del mondo reale troviamo dataset con decine di feature.
Vuoi perché il nostro stakeholder ci abbia fornito l’intero database di produzione aziendale, o per il semplice fatto che si è deciso di tenere ogni colonna e non perderne nemmeno una, al momento della creazione del modello predittivo dobbiamo affrontare una sfida niente male.
Tendenzialmente iniziamo a lavorare con modelli semplici, ben lontani dalle complicate reti neurali.
Ricorda infatti che le Neural Network non sono la soluzione a ogni problema.
Ora dobbiamo tenere presente che i modelli di regressione lineare (tra i più semplici) difficilmente vengono usati in applicazioni concrete per due ragioni:
- Faticano a esprimere relazioni non lineari
- Tendono all’overfitting quando il numero di feature aumenta
Gli Alberi Decisionali (Decision Trees) possono risolvere il primo problema, per il secondo dobbiamo invece indagare più a fondo.
Il problema è che un modello di regressione lineare ha pochi gradi di libertà (degrees of freedom): quando questi aumentano, la complessità del modello aumenta, e con essa il rischio di overfitting.
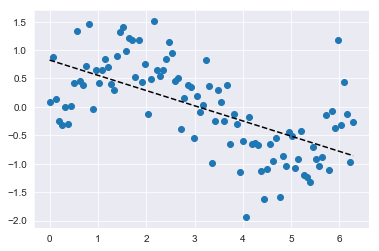
Intuitivamente i gradi di libertà sono i punti in cui la funzione si flette, e curva.
Quando usiamo un modello di regressione lineare applicato, ad esempio, a 100 feature, questo è quello che succede:
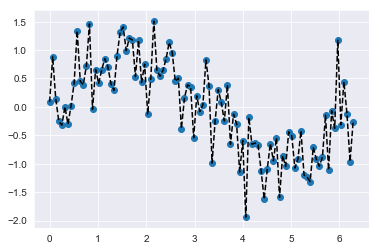
Per tracciare il grafico ho generato dei numeri randomici, puro rumore, che simulano però la presenza di feature inutili nel dataset (cosa molto comune).
Per risolvere questo problema, entra in gioco Ridge Regression.
Ridge Regression: how?
Abbiamo capito perché sia importante, ora svisceriamone il funzionamento.
Ridge Regression aggiunge un fattore di penalizzazione (penalty factor) alla cost function. Ciò determina la perdita d’importanza del valore di una feature, che a seconda della penalità, può essere più o meno accentuata.La forza della penalità è tunable controllata cioé da un hyperparameter che deve essere setato.
Parlando di regolarizzazione in generale esistono due tipi di penalizzazione:
- L1 (absolute size) penalizza il valore assoluto dei coefficienti del modello
- L2 (squared size) penalizza il quadrato del valore dei coefficienti del modello.
Ridge Regression usa la L2 penalty
In pratica questo produce coefficienti piccoli, ma nessuno di loro è mai annullato. Quindi i coefficienti non sono mai 0. Il fenomeno è denominato feature shrinkage.
Ridge Regression Sklearn
Teoria a parte, è arrivato il momento di prendere in mano un po’ di codice.
Qui puoi trovare la documentazione di sklearn, mentre di seguito ti faccio vedere come importare il tutto velocemente:
from sklearn.linear_model import Ridge ridge = Ridge(alpha=0.1) ridge.fit(x_train,y_train) ridge.score(x_test,y_test)
Un caldo abbraccio, Andrea.




