La Matrix Factorization o fattorizzazione di matrice è una classe di algoritmi per il collaborative filtering usata nei sistemi di raccomandazione.
Nel nostro precedente post sui Recommender System abbiamo palesato la differenza sostanziale tra i sistemi Content-Based e quelli di Collaborative Filtering.
Quest’ultima classe di sistemi risulta spesso essere l’opzione più scelta: un metodo sofisticato per generare raccomandazioni utenti.
Oggi vediamo insieme un algoritmo che ne permette l’ottimizzazione e spieghiamo perché il Matrix Factorization è da tenere in considerazione nel processo di development di un reccomender system.
Why?
Pensiamoci un attimo.
Avere uno scopo è fondamentale.
Tanto nella complessità della vita quanto in questo piccolo post.
Per il capire il perché, dobbiamo allora fare un passo indietro.
Sai quale forma ha un dataset per un sistema di raccomandazione?
Non ti preoccupare. Eccolo qui:
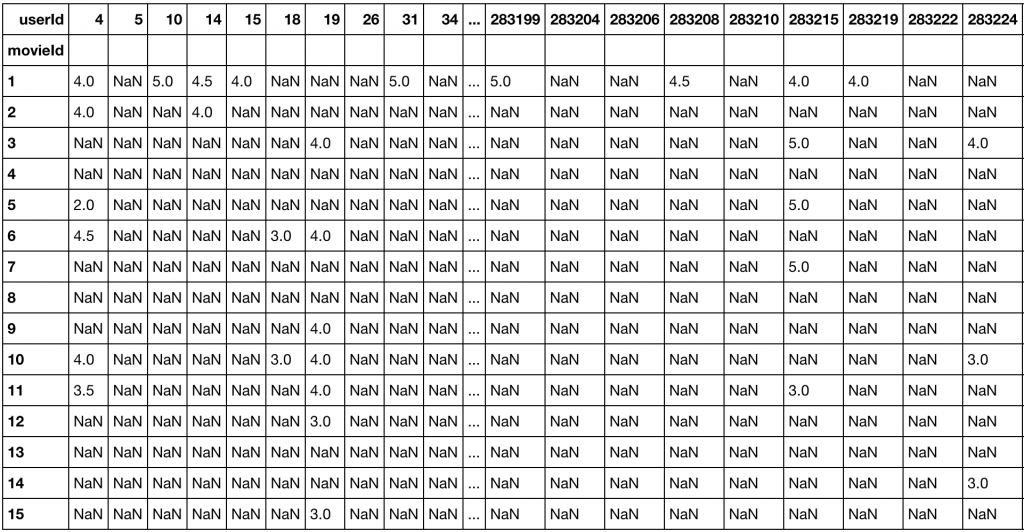
Il dataset può essere rappresentato come una matrice d’interazione tra entità.
Un esempio comune?
Per la creazione di un sistema di raccomandazione di film, la matrice è data da interazioni utente-film (o film-utente) in cui ogni riga rappresenta un utente i e ogni colonna un film j.
Quindi ogni entità nella matrice cattura una preferenza o valutazione utente per uno specifico elemento: un video, un prodotto, un articolo etc.
In un mondo perfetto, avremmo tutti i dati per procedere.
Nel mondo reale… beh le cose si complicano un po’.
Considerando l’esempio iniziale, la maggior parte dei film avrebbe poche o nessuna recensione: quindi la matrice si configurerebbe come estremamente sparsa (sparse matrix), e senza esagerare troppo… con più del 99% delle entità mancanti.
Con una così bella matrice… quale machine learning algorithm riuscirebbe mai a fare inferenza in modo affidabile?
Per trovare una soluzione dobbiamo risolvere quello che si configura come un data sparcity problem.
Matrix Factorization
Nel campo del Collaborative Filtering, il Matrix Factorization è la soluzione stato dell’arte (state-of-the-art) allo sparse data problem.
Una soluzione questa, divenuta celebre nel Netflix Prize Challenge, il quale è riuscito a mettere in luce anche alcune gravi falle nel sistema di privacy preserving.
La parte che segue è molto importante, seguimi attentamente.
Latent Factors
La Matrix Factorization assume che esista una serie di attributi (set of attributes) comune a tutti gli Items, che differiscono dal grado di espressione di quegli stessi attributi.
In più, ogni User ha la propria espressione degli stessi attributi, in modo indipendente dagli Items.
Così la valutazione di uno User è approssimata dalla somma del valore di ciascun attributo, pesata dal grado di espressione dello stesso da parte del’Item.
Inoltre, devi sapere che questi attributi sono spesso definiti fattori latenti (latent factors), o nascosti.
Nel caso di un film, questi fattori latenti sono il genere, il cast di attori, e il regista per citarne alcuni.
Come può la fattorizzazione della matrice risolvere il nostro problema originale?
Due punti.
- Il modello impara a fattorizzare le recensioni in rappresentazioni di utenti e film, che gli consentono d’inferire con maggiore accuratezza
- Con la fattorizzazione di matrice, film meno noti (con un numero esiguo di recensioni) possono avere tanti fattori latenti quanto quelli più conosciuti, aumentandone la raccomandazioni.
Represent Latent Factors
Preparati.
Stiamo per rispondere alla domanda iniziale: che cos’è il matrix factorization?
Semplicemente, possiamo ora dire che si tratta di una famiglia di operazioni matematiche di algebra lineare per operare sulle matrici.
Più nel dettaglio, una fattorizzazione di matrice scompone quella originale in due nuove matrici.
Nel caso del Collaborative Fltering, l’algoritmo di matrix factorization decompone le interazioni user-item nel prodotto di due matrici rettangolari dalla dimensionalità inferiore.
Per tradurre l’esistenza di fattori latenti nella matrice di ratings compiamo alcune opreazioni:
- Per un gruppo di utenti U di dimensioni u e elementi I di dimensioni i consideriamo un numero arbitrario k di fattori latenti.
- Fattorizziamo ora la matrice R iniziale in due matrici rettangolari più piccole.
- Otteniamo una matrice X (row factor) e una matrice Y (column factor).
- La matrice X ha dimensioni u*k e quella Y, k*i
In algebra lineare, compiamo un’operazione detta di Low-Rank Approximation.
Di queste due nuove matrici, la prima ha una riga per ogni user mentre la seconda una colonna per ciascun item.
Moltiplicando le matrici tra loro, otteniamo una nuova matrice R’ che è un’approssimazione della prima.
Dimensionality Reduction
Il numero di fattori latenti non è determinato a priori, e viene regolato anche attraverso tecniche di cross validation.
In altre parole, i fattori latenti sono feature dello spazio latente dalla dimensionalità inferiore e costituiscono la proiezione delle interazioni user-item della matrice originaria.
L’idea è quindi quella di semplificare lo spazio di operazione del modello, riducendo la complessità dei dati.
Ogni utente, ed elemento, è rappresentato da un vettore in questo spazio k-dimensionale, in cui ciascuna riga in X corrisponde al valore dell’espressione dei fattori latenti per l’Utente, mentre per le colonne in Y troviamo l’espressione degli stessi da parte degli Item.
Per calcolare la valutazione di un utente u su un prodotto i, effettuiamo il dot product dei due vettori:
Il risultato è l’approssimazione, o in termini più coretti la previsione della valutazione dell’utente per l’Item
L’algoritmo di Matrix factorization può dunque essere considerato una tecnica di dimensionality reduction, come la PCA (Principal Component Analysis).
Vedi.
Il numero di fattori latenti determina l’ammontare d’informazione astratta che vogliamo mantenere in uno spazio di dimensionalità inferiore.
Una fattorizzazione di matrice con un solo fattore latente equivale alla raccomandazione di un item con il maggior numero d’interazioni, senza alcuna personalizzazione.
Per migliorare quest’ultima occorre invece incrementare i latent factor, prestando attenzione alla loro crescita.
Quando il numero diventa troppo alto, il modello entra in overfitting. Più dettagli qui.
Regularization and troubleshooting
Una strategia comune per arginare il problema è il ricorso a termini di regolarizzazione.
Abbiamo visto un esempio di regularization trattando il Ridge Regression, che ci ha permesso di chiarire quali grandi tipologie di regolarizzazione esistano.
Mi raccomando, dai un’occhiata qui: così puoi capire meglio di cosa parliamo!
Tornando a noi…
Nel nostro caso l’objective function diventa quella funzione che determina il delta tra la valutazione prevista e quella reale, valore che deve essere minimizzato grazie all’algoritmo di Matrix Factorization.
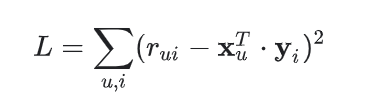
Hai presente cos’è un algoritmo di ottimizzazione?
Ottimo, ora che abbiamo ripassato il concetto possiamo proseguire.
Definita la funzione costo abbiamo bisogno di un algoritmo di ottimizzazione per completare l’implementazione di Matrix Factorization.
Matrix Factorization: Funk SVD
Il primo a proporre un’implementazione di questo tipo fu Simon Funk, e prese per questo il nome di Funk SVD.
Per concludere l’argomento regolarizzazione, devi sapere che il Funk SVD ne implementa una di tipo L1.
Il Funk SVD ha un unico grande problema.
Non è scalabile.
Con l’ammontare del volume dati odierno, le prestazioni rapidamente degradano.
Quando Simon lo presentò alla community nel 2006, il sistema era molto efficiente su singola macchina.
Come possiamo allora ottenere la massima resa dell’implementazione, arginando il problema della scalabilità?
Dobbiamo distribuire il lavoro di training.
Abbiamo quindi bisogno di un framework attraverso cui allenare un modello di machine learning su più macchine, creando una rete o cluster di macchine: il distributed computing, o calcolo distribuito.
A soccorrerci, entra in gioco una tecnica denominata ALS: Alternating Least Square.
Vediamola insieme!
Per approfondire matrix fatcorization, dai invece un’occhiata qui.
Per il momento è tutto.
Un caldo abbraccio, Andrea.




