Homomorphic Encryption è una forma di criptazione che permette di eseguire calcoli su operandi criptati, ottenendo un risultato criptato.
Una volta decriptato il risultato, questo risulta identico a quello ottenuto effettuando lo stesso calcolo sugli operandi reali e non criptati.
Secret Sharing è una tecnica in base al quale un segreto x è diviso in molteplici quote (share) che vengono poi distribuite a un gruppo di secret-holder.
Il segreto x può quindi essere ricostruito solo quando tutte le quote in cui è stato diviso sono disponibili.
Le nostre amate definizioni introduttive.
Ora andiamo al succo. Facciamo un esempio.
Siamo proprietari di un’informazione, un numero x che dividiamo in 3 quote: x1, x2, x3. Inizializziamo casualmente le prime due, e calcoliamo la terza quota come:
x3 = x -( x1 + x2)
Distribuiamo quindi le nostre 3 quote (share) ad altrettanti secret-holder. Il segreto iniziale, il nostro numero x, rimane nascosto a ciascun individuo poiché ognuno di loro possiede una sola share e non ha idea del valore totale.
La procedura può essere resa più sicura scegliendo il range di valori validi per le share. I numeri primi accorrono in nostro soccorso.
Definiamo Q un numero primo grande quale limite superiore. Ora la nostra terza share sarà definita da:
x3 = Q - (x1 + x2) % Q + x
Poiché in questo post andremo dritti alla parte pratica, ecco il codice python per compiere un’operazione simile:
import random
# setting Q to a very large prime number
Q = 23740629843760239486723
def encrypt(x, n_share=3):
r"""Returns a tuple containg n_share number of shares
obtained after encrypting the value x."""
shares = list()
for i in range(n_share - 1):
shares.append(random.randint(0, Q))
shares.append(Q - (sum(shares) % Q) + x)
return tuple(shares)
print("Shares: " + str(encrypt(3)))Ecco una rappresentazione visiva della divisione di x in tre share usando un numero Q come upper limit
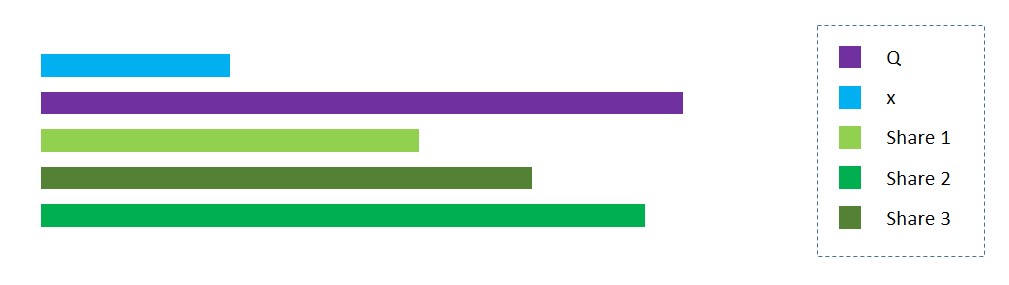
La funzione di decriptazione sarà semplicemente la somma delle quote in modulo Q:
def decrypt(shares):
r"""Returns a value obtained by decrypting the shares."""
return sum(shares) % Q
print("Value after decrypting: " + str(decrypt(encrypt(3))))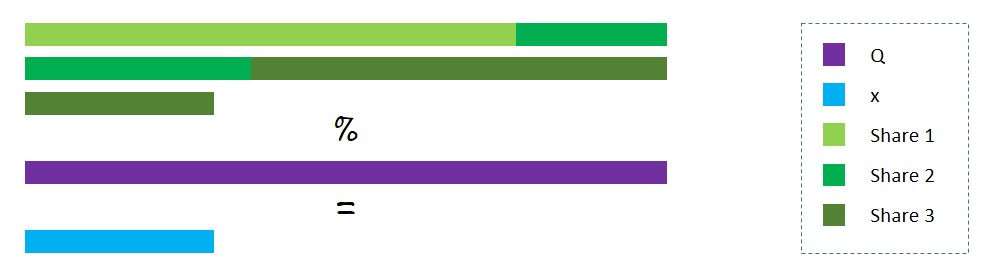
Ora, il sistema di secret sharing che abbiamo definito è più precisamente di Additive Secret Sharing, una tecnica che contiene di per sè l’homomorphic encryption.
Dividiamo x in x1,x2,x3 e y in y1,y2,y3 allora è vero che:
x + y = (x1 + y1) + (x2 + y2) + (x3 + y3)
Codice? Presto detto:
def add(a, b):
r"""Returns a value obtained by adding the shares a and b."""
c = list()
for i in range(len(a)):
c.append((a[i] + b[i]) % Q)
return tuple(c)
x, y = 6, 8
a = encrypt(x)
b = encrypt(y)
c = add(a, b)
print("Shares encrypting x: " + str(a))
print("Shares encrypting y: " + str(b))
print("Sum of shares: " + str(c))
print("Sum of original values (x + y): " + str(decrypt(c)))Siamo quindi in grado di calcolare la somma di due valori senza conoscere il valore reale di ognuno di essi.
Yea.
PySyft ci consente di padroneggiare queste tecniche e sviluppare modelli che tengano conto di homomorphic encryption e additive secret sharing
Fonte: OpenMined
Un caldo abbraccio, Andrea




