Cos’è il Gradient Descent (Discesa del gradiente) ? Il Gradient Descent è un optimization algorithm (algoritmo di ottimizzazione) capace d’individuare il valore minimo di una cost function, consentendoti di sviluppare un modello dalle accurate previsioni.
Allineiamoci un attimo.
Oversimplifying… Una rete neurale sviluppa una funzione che mappa gli input agli output e viene generato un modello utile a fare previsioni.
Quella funzione contiene differenti parametri il cui valore deve essere in qualche modo appreso.

Siamo data scientst. Siamo mucche viola. Il nostro codice etico reclama un linguaggio forbito.
Prima di arrivare a una spiegazione tecnica, dobbiamo comprendere il concetto intuitivamente.
Dunque.
Calcolare valori randomici a ogni epoca, o iterazione, con il solo obiettivo di generare quelli perfetti è il modo stupido di procedere. Non ci piace.
In realtà conserviamo il metodo randomico per inizializzare i parametri.
Ora però dobbiamo valutare in che modo la loro variazione cambi la previsione finale.
Ci serve quindi una funzione che determini quanto il nostro modello sia bravo, o meno, a effettuare le previsioni: entra in gioco la cost function.
Piccola nota: loss function e cost function sono concetti differenti. In breve, senza scendere troppo nel tecnico, la loss function è relativa alle singole previsioni, quindi calcolata su ciascuna osservazione del dataset; la cost function è definita globalmente.
Quindi ora abbiamo:
- Una funzione con il compito di mappare gli input e gli output: il nostro modello, con differenti parametri i weights.
- Una cost function che calcola quale sia l’errore del modello per i parametri che lo definiscono.
Ecco la strada per arrivare in vetta: dobbiamo minimizzare la cost function, cioè trovare quei valori del modello, quei weights, tali per cui la cost function abbia il valore minimo.
Come facciamo?
Ancora una volta entra in gioco la matematica e come sempre con una soluzione brillante: optimization algorithm, ovvero gli algoritmi di ottimizzazione.
Abbiamo definito cosa siano, e chiuso la nostra introduzione con una carrellata di algoritmi.

Abbiamo definito cosa siano, e chiuso la nostra introduzione con un cestino di algoritmi.

Gradient Descent algorithm
Finalmente iniziamo a parlare di Gradient Descent.
Ripetendoci, ma principalmente per motivi estetici:
Gradient Descent (Discesa del gradiente) è un optimization algorithm (algoritmo di ottimizzazione) generico capace d’individuare il valore minimo di una cost function, consentendoti di sviluppare un modello dalle accurate previsioni.
Gradient descent definition
Il cliché vuole che per descriverne il funzionamento si usi la metafora della montagna con la nebbia.

Ormai mucche viola al pascolo, un po’ di nebbia in montagna può farci solo che bene.

Nel problema della montagna vogliamo raggiungere il punto più basso, la valle. La difficoltà è data dall’impossibilità di vedere il tragitto. Quindi decidiamo di procedere a tentativi testando il terreno e la sua pendenza.
Quando inizieremo a salire, la nostra discesa sarà terminata e avremo raggiunto il punto di minimo.
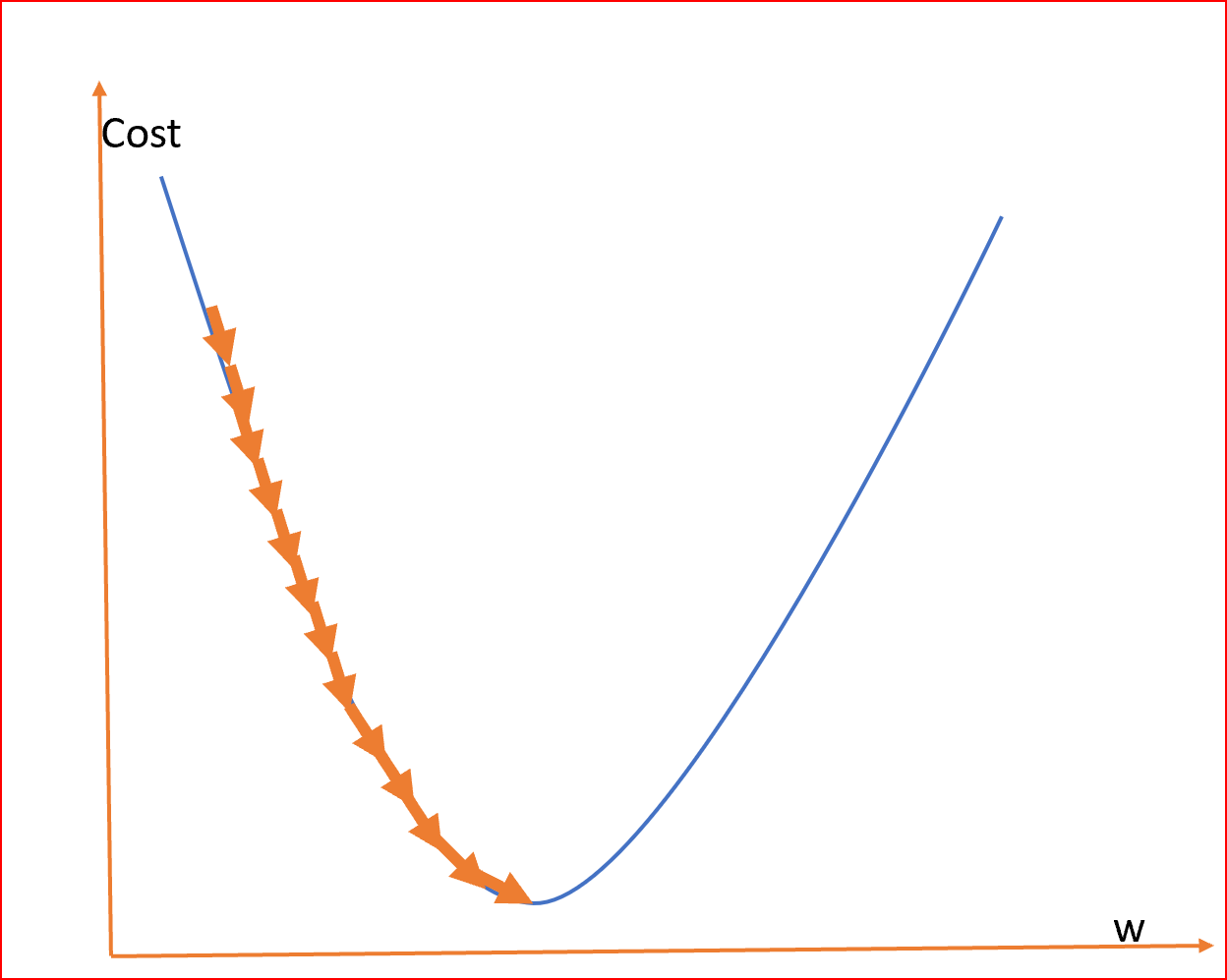
Come accennato poco fa, la best practice prevede l’inizializziazione in modo randomico dei weights ad un valore prossimo allo zero, ma non zero. (random initialization)
Ora introduciamo un termine: il gradiente.
Il gradiente indica la direzione di salita, quindi è nostro interesse ottenere un gradiente negativo, perché vogliamo scendere, vogliamo raggiungere il punto di minimo.
Quindi aggiorneremo (update) i weights nella direzione negativa del gradiente (negative gradient direction) per minimizzare la perdita (to minimize the loss).
Di quanto deve essere aggiornato il valore?
Lo stabilisce il learning rate.
In soldoni, Il learning rate è un hyperparameter che influenza il cambiamento dei weights in funzione del gradiente.
Approfondiremo insieme questo concetto in un altro post.
Ti basta sapere che il learning rate gestisce lo step di cambiamento dei parametri a ogni iterazione, e viene generalmente indicato con la lettera greca α :
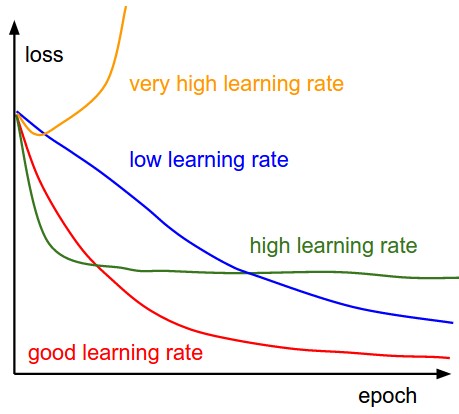
- Per α troppo piccolo, il tempo di convergenza (convergence) è grande, quindi la determinazione del punto di minimo impiega parecchie risorse computazionali.
- Per α grande, potrebbe fallire la convergenza, superando il minimo, o arrivando persino a divergere mancando la determinazione della soluzione.
Minimo locale o globale?
Non tutte le funzioni di costo sono semplici archi.
Questo rende l’individuazione del minimo piuttosto complessa.
In merito alla metafora della montagna, potresti infatti obiettare affermando che la “valle” identificata, sia un minimo locale, ben lontana dal nostro ideale minimo globale.

La nostra amata montagna ci tende un trabocchetto e la valle che crediamo di aver raggiunto è in realtà un ampio terreno pianeggiante: siamo ancora in alta quota, la pianura è altrove.
Prendiamo un esempio pratico.
La Mean Squared Error, una cost function spesso impiegata nel modello di Linear Regression, è una funzione convessa (convex function).
Una convex function ci piace per tre motivi:
- Ha un minimo globale, senza alcun minimo locale
- La random initialization non compromette la convergenza
- È una funzione continua, questo implica che la sua derivata sia una funzione Lipshitziana.
Queste qualità, unite a un learning rate non troppo alto, garantiscono la convergenza al minimo globale. (dopo un tempo sufficiente).
In generale però, come può il gradient descent riconosce un minimo locale da uno globale?
Short answer non può.
Long answer lo rendiamo possibile.
Esistono infatti metodi alternativi per ovviare a questa insidiosa problematica.
Vediamoli nel prossimo post!
Un caldo abbraccio, Andrea.