In questo post analizzeremo alcuni concetti importanti del Deep Reinforcement Learning: il Q-learning e il Deep Q-Learning.
Prima d’iniziare, lascia che ti presenti una brevissima introduzione al Reinforcement Learning.
Il Reinforcement Learning è un processo caratterizzato da due entità:
- Un ambiente (environment) che semplifica una certa realtà
- Un agente (agent), tecnicamente un modello di AI (e.g. rete neurale) che interagisce con l’ambiente.
Ci sono altri tre termini chiave nel vocabolario del Reinforcement Learning che devi necessariamente conoscere.
Poco fa ti ho detto che l’agente interagisce con l’ambiente.
Per realizzare ciò, compie azioni (actions) che alterano l’ambiente generando un nuovo stato (state), ottenendo una ricompensa (reward) che può essere negativa o positiva in base all’effetto dell’azione, e in funzione del risultato desiderato.
Compiendo azioni e ottenendo ricompense, l’agente elabora una strategia ottimale per massimizzare la ricompensa nel tempo. Questa strategia è definita policy, ed è una funziona matematica a parametri ottimizzati.
Bellman Equation per Q-Learning
L’Equazione di Bellman è un concetto fondamentale nel Renforcement Learning,
Fu introdotta nel 1954 dal Richard Bellman, conosciuto come il padre del Dynamic Programming, in una pubblicazione intitolata The Theory of Dynamic Porgramming.
Lascia quindi che ti spieghi perché sia così importante.
Partiamo da un Toy Problem, un problema piccolo e utile solo a capire i concetti di fondo.
Consideriamo un piccolo robot che debba raggiungere la posizione finale di un percorso evitando gli ostacoli:
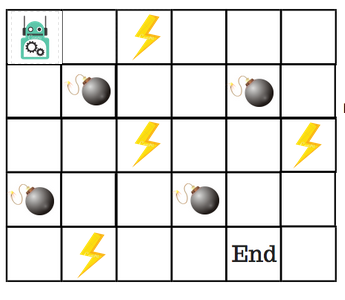
Potremmo quindi configurare un sistema a ricompense specifico per l’ambiente tale per cui:
- -1 per ogni step (Per incoraggiare l’agente a raggiungere l’obiettivo percorrendo la tratta più breve)
- -100 per ogni mina
- +1 per ogni fulmine
- +100 per il raggiungimento della fine.
Per risolvere questo problema, dobbiamo introdurre il concetto di Q-Table.
Q-Table
Una Q-Table è una lookup table che calcola il valore atteso delle ricompense future per ogni azione in ogni possibile stato. Questo permette all’agente di scegliere la migliore azione in ogni stato.
Il nostro ambiente ha 4 possibili azioni (sopra, sotto, destra, e sinistra) e 5 possibili stati (inizio, vuoto, fulmine, mina, fine).
La domanda è dunque: come calcoliamo la massima ricompensa possibile per ogni stato, ovvero i valori della Q-Table?
Abbiamo bisogno di un processo iterativo che faccia uso del Q-Learning algorithm, il quale a sua volta si appoggia all’equazione di Bellman.
E il cerchio si chiude.
L’Equazione di Bellman per sistemi deterministici è la seguente:
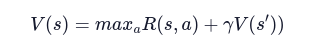
In cui abbiamo:
- s – State
- α – Action
- R – Reward
- γ – Discount factor
Il fattore di sconto è necessario per tarare la variazione della ricompensa nel tempo, comunicando all’agente quanto sia rilevante la ricompensa presente rispetto a quella futura.
C’è però una questione limitante nell’applicare l’equazione a qualsivoglia ambiente.
La formula funziona solamente quando è noto lo stato successivo, informazione spesso sconosciuta e anzi dipendente dall’azione compiuta.
Abbiamo quindi bisogno di un sistema per modellare ambienti in qualche modo legati a un fattore casuale, non prevedibile.
Ora che abbiamo un’infarinatura sul concetto di Q-Table, passiamo quindi al prossimo: i Markov Decision Processes
Markov Decision Processes (MDPs) in Q-Learning
Dobbiamo distinguere due tipologie di ambiente:
- Ambiente Deterministico, per ogni azione compiuta dall’agente la probabilità che questa avvenga correttamente è massima (100%)
- Ambiente non deterministico, per ogni azione compiuta dall’agente la probabilità che questa avvenga è influenzata da un fattore casuale, ed è quindi incerta.
Ora possiamo allora introdurre il concetto di processo di Markov e processo decisionale di Markov.
Abbiamo approfondito l’argomento nel post su Tutto sul Markov Decision Process, quindi saremo veloci qui.
Processo di Markov è tale quando presenta la proprietà di Markov, quando cioè la distribuzione di probabilità dei futuri stati del processo dipendono unicamente dallo stato presente e non dalla serie di eventi a esso preceduti.
I processi decisionali di Markov costituiscono invece un framework per modellare, sotto specifiche condizioni, un atto di Decision Making, in quelle situazioni in cui il risultato è in parte casuale e in parte sotto il controllo del decision maker.
Applicando questi concetti all’Equazione di Bellman, otteniamo una variante per ambienti non deterministici:
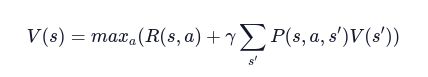
Q-Learning
Con le nozioni di Equazione di Bellman e di Markov Decision Process sulle spalle possiamo finalmente sviscerare il concetto di Q-Learning.
Fin’ora abbiamo cercato di calcolare V(s), con il quale derivare la migliore azione da compiere in funzione dello stato corrente.
Ora invece di considerare il valore di ogni stato V(s), prendiamo il valore della coppia stato-azione che indichiamo con Q(s,a).
Intuitivamente, possiamo pensare al Q-value come la “qualità”dell’azione.
La nostra equazione diventa quindi:
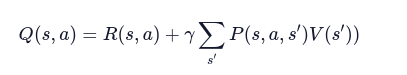
Compiendo un’azione, il nostro agente riceve inizialmente una ricompensa R(s,a) .
Ora poiché il nuovo stato può esse uno tra molti, aggiungiamo il calcolo del valore atteso nello stato successivo.
Per cui il valore dello stato V(s) assume il massimo valore tra tutti i possibili Q-values.
Con una semplice modifica, otteniamo dunque la formula ricorsiva per il calcolo del Q-Value.
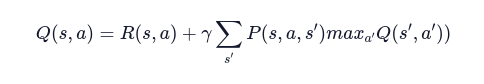
Sappi che, sebbene l’esempio sia caratterizzato da uno spazio azioni e stati discreto, lo stesso ragionamento può essere applicato a uno spazio azioni e stati continuo, generalmente dividendo il continuo in intervalli discreti.
Per il momento è tutto.
Per aspera, ad astra.
Un caldo abbraccio, Andrea




