Per processare che entrano in un neurone artificiale si usano spesso due paraetri: il bias e il weight. Oggi vediamo l’importanza del weight in una rete neurale artificiale! Towards Machine Learning!
Perceptron
Nel 1943 McCulloch and Pitts rappresentarono matematicamente (dunque in modo artificiale) un neurone. Questo modello prese il nome di perceptron.
L’obiettivo era quello di creare un modello artificiale, sufficientemente semplice ma al contempo efficacemente esplicativo, di un neurone biologico.
Nel 1958 Rosenblatt ideò un sistema per allenare il perceptron.
Il perceptron è spesso considerato la più basica forma di una rete neurale artificiale (Artificial neural network), ed è quindi particolarmente utile per fini didattici, come il nostro.
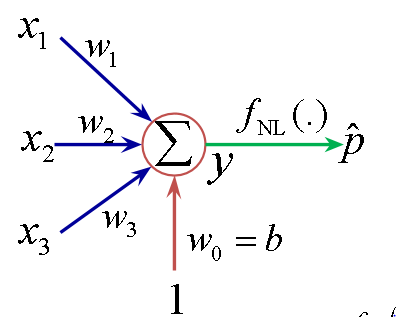
Un perceptron su singolo layer, come quello nell’immagine, agisce da classificatore binario lineare.
Cosa significa? Che lavora con 0 e 1, e produce un output che può essere 0 o 1.
Per computare un output, sono ammesse diverse tipologie di azioni:
- somma degli input O = [x1, x2, x3, xn]
- applicazione di un’operazione lenare O = [(x1*x2)+x3]
Ed ecco che iniziano le difficoltà.
Ricordi che poco fa abbiamo definito il perceptron come un semplice ed essenziale classificatore binario? Cosa succede se applichiamo un’operazione matematica come il prodotto e lavoriamo con lo zero?
Casini. Succedono casini.
Prendendo in considerazione la seconda tipologia di operazione tra quelle presentate, l’output sarà x3 anche se solo uno tra x1 e x2 è zero.
Tradotto, è possibile incorrere in perdita di informazioni. Spesso, questo non è ammissibile.
Si potrebbe pensare che per eludere il problema sia sufficiente abbandonare la moltiplicazione in favore di una meno problematica somma.
La soluzione è parziale, il problema di fondo resta:
il peso degli input, in termini di importanza non è quantificato.
Il Weight: dare un peso ai dati
Consideriamo un semplice esempio.
Vogliamo creare un perceptron per fare una previsione meteorologica. Definiamo il dato:
- x1 come indicatore di umidtà: umido (1), non umido (0);
- x2 sarà invece 1 se indossi un cappello verde e 0 se non lo indossi
Come il buono senso consiglia, x2 non ha valore nella nostra previsione.
Come facciamo però a dire al nostro perceptron che il valore dell’informazione trasmessa da x2 è basso?
Ecco che entra in gioco il weight!
In questo modo, se è umido e indossiamo un cappello verde:
[ex 1] O = x1+w2*x2 = 1+0.1*1 = 1.1
Oppure, se è umido ma non indossiamo il cappello:
[ex 2] O = x1+w2*x2 = 1+0.1*0 = 1
Così facendo, l’informazione è preservata ma la sua importanza viene ponderata. Dal momento che pesiamo l’informazione, nel senso che diamo più o meno peso al valore di un dato in input, definiamo il parametro weight.
Il Bias: la threshold
In questo precedente post abbiamo visto insieme quale sia l’importanza di avere un parametro come il bias.
Riprendo il discorso e mi collego a quanto detto poco fa per chiarire ulteriormente il concetto di bias!
Se osservi [es 1], puoi notare una stranezza.
Abbiamo detto che il perceptron è un classificatore binario, ma la nostra somma resituisce 1.1 . Come gisutifichiamo questo valore se i soli possibili sono 1 e 0 ?
Che ne dici, impostiamo una threshold? Metti! Metti! E impostiamola!
Quindi:
[ex 3] O = 1 => se (x1 + x2*w2) >= 1
[ex 4] O = 0 => se (x1 + x2*w2) < 1
Ora generalizziamo il tutto:

E semplifichiamo la notazione matematica per chiarificare il tutto:

- b, comunemente usato in riferimento al bias, è l’opposto della threshold




