Prepariamoci ad approfondire il concetto di circuito aritmetico.
Stai per iniziare un viaggio che ti accompagnerà alla scoperta di affascinanti concetti della crittografia, con l’obiettivo ultimo di comprendere come funzionino alcune delle più innovative blockchain pubbliche.
Il circuiti aritmetici, o circuito aritmetico al singolare, (giusto un paio di ripetizioni per soddisfare le esigenze SEO) costituiscono un elemento chiave per comprendere appieno le zk-snarks, che abbiamo analizzato in un passato articolo.
Per capire cos’è un circuito aritmetico dobbiamo prima introdurre il concetto di campo finito.
Il campo finito
Detto anche campo di Galois, un campo finito è una struttura algebrica composta da un insieme non vuoto e da due operazioni binarie interne chiamate somma e prodotto.
Tradotto in soldoni, è un artificio che i matematici si sono inventati per risolvere problemi complessi. E sebbene al momento qualsiasi esempio ti facessi renderebbe il campo finito una complicazione eccessiva, ti posso assicurare che a breve la sua forza risulterà emozionante.
Seguimi.
Senza scendere troppo nei dettagli, consideriamo il nostro campo finito F dato dall’insieme dei numeri compresi tra 0 e p-1. In questo campo svolgeremo operazioni di addizione e moltiplicazione in modulo p.
Consideriamo ora alcuni numeri primi maggiori di 2, quindi p > 2. Abbiamo ora nella nostra testa un campo finito primo (prime finite field)
Ora che abbiamo aggiunto il concetto di campo al nostro bagaglio culturale possiamo definire un circuito aritmetico come un grafo diretto aciclico (DAG, Directed Acyclic Graph) dove i nodi interni (definit anche gates) sono operazioni di somma, differenza e prodotto, mentre gli input sono numeri compresi tra x1 e xn e la costante 1.
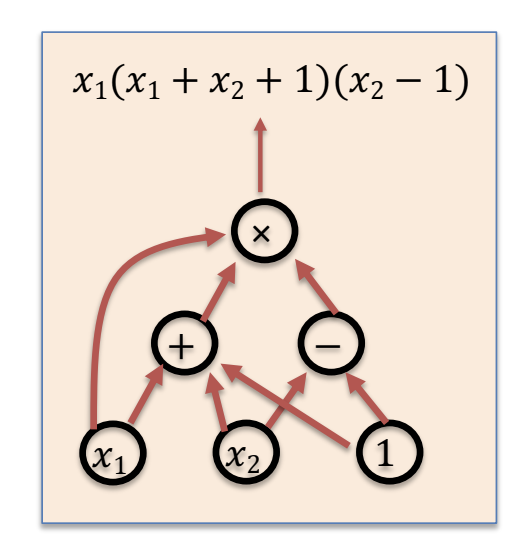
Sono sicuro che il tuo livello di confusione sia solo aumentato. Lascia allora che cambi il punto di vista. Non abbiamo fatto altro che rappresentare un polinomio complesso (n-variate) in una forma che ne indichi la risoluzione, il grafo appunto.
Dati X1 e X2 possiamo infatti seguire le frecce del grafo e calcolare il valore del polinomio.
Di questa interessante spiegazione dobbiamo poi fossilizzare il fatto che la dimensione del circuito è data dal numero di gates (nodi interni) del circuito. Nell’esempio, la dimensione è 3. Quello per calcolare un hash base ne ha circa 20000. (Capisci perché tornano utili?). La formula con cui indichiamo la dimensione del circuito aritmetico è la seguente:
|C| = # gates in C
Ora possiamo finalmente rispondere alla domanda che un qualsiasi ingegnere si sta ponendo dall’inizio. Ma a che cavolo serve questo grandissimo figlio di circuito?
A cosa serve un circuito aritmetico?
I matematici si sono resi conto che attraverso un circuito aritmetico è possibile rappresentare, per certi versi, qualsiasi calcolo a complessità computazionale polinomiale.
In questo ampio insieme di operazioni a noi interessano principalmente quelle di hashing. Facciamo un esempio considerando un circuito aritmetico di hashing. Questo circuito ha due input, un hash value h e un hash input m e restituisce 0 se e solo se il SHA256 di m è uguale a h, o un numero diverso da 0 altrimenti (leggi la prima riga).

Possiamo allora semplificare la rappresentazione del circuito con la seconda riga, in cui banalmente diciamo che se h equivale a SHA256 di m, la differenza è 0. Un circuito del genere ha 20000 gates circa. Per intenderci non è un grande circuito.
Ora consideriamo una seconda funzione ben più complessa. Una funzione di signature verification, fondamentale in ogni blockchain.
Un circuito aritmetico di una funzione di verifica della firma avrà come input una chiave pubblica, un messaggio (m) e una firma (sigma, σ) e produrrà 0 se la firma è valida (in questo caso una valida ECDSA) sul messaggio m data la chiave pubblica.

Per il momento è tutto.
Per aspera, ad astra.
Un caldo abbraccio, Andrea



